진수 변환

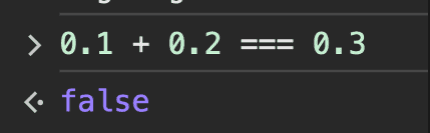
JavaScript 에서 0.1 + 0.2 === 0.3 을 검사해보면 false 가 나온다.
아니 더 정확하게는 JavaScript뿐만 아니다.
이유가 뭘까?

오늘은 기술면접에서도 종종 등장하는 0.1 + 0.2 에 대한 문제에 대해 얘기해본다

우선 우리가 사용하는 컴퓨터는 2진법 이라는것을 사용한다. 사람은 0~9 까지 표현할 수 있는 10진법 을 사용하는데 반해 컴퓨터는 모든 정보를 1 또는 0 으로 표현한다.

10진법을 2진법으로 혹은 2진법을 10진법으로 바꾸면 어떤일들이 일어날까?

정수의 2진수 변환

10진수를 2진수로 바꾸는 방법은 간단한다.
2로 나누면서 남는 몫을 순서대로 적으면 된다.
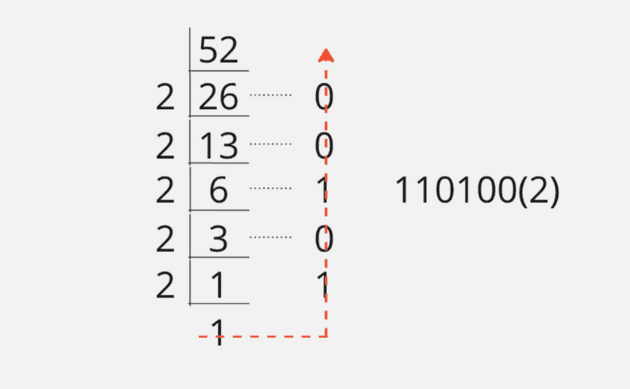
예를들어 52(10) 을 2진수로 바꿔보다.

`(10)` 또는 `(2)` 라는 표현은 각각 10진수, 2진수 임을 나타낸다.

52를 이진수로 변환하면 그림과 같은 순서로 110100 (2) 로 표현할 수 있다.
정수는 아주 간단한다.

그렇다면 소수가 포함되어있는 실수의 경우엔 어떨까?
컴퓨터에서 실수의 경우에는 소수점을 기준으로 정수, 소수점을 나누어서 계산해야 한다.
정수는 위에서 설명한 방법대로 2진수로 변환하기때문에 문제가 없다.

그렇다면 소수는 어떨까?

소수의 2진수 변환

정수와 반대로 소수는 2를 나누는게 아니라 2를 곱하면서 계산해주어야 한다.

0.625를 예로 들어보자

2씩 곱하고 몫을 남겨두고 나머지를 다시 2를 곱하는 방법의 반복으로 2진수를 구할 수 있다.

결과는 101 (2)
위의 52에 0.625를 더한 즉, 52.625 는 110100.101 (2) 로 표현할 수 있다.
0.625와 같이 딱 나누어 떨어지는 숫자라면 항상 해피하다.

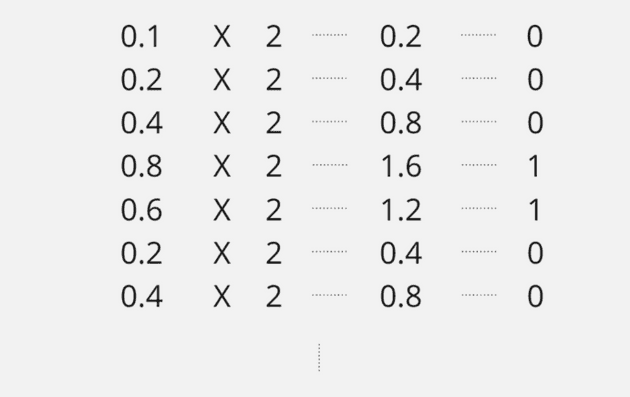
0.1 이라는 소수의 경우엔 어떨까?

딱 나누어 떨어지지 않고 연산이 무한대 이어지게 된다.

우리의 컴퓨터 메모리 공간에는 무한한 값을 저장할 수 는 없다. 그렇다면 언젠가 무한대로 이어지는 연산의 끝을 구해야 할테고 결국엔 언젠가는 특정 자리에서 반올림 해야할 것이다.

그렇다면 그 특정 자리 는 언제일까?

무한하게 이어지는 연산의 끝이 어딘지 알기 위해서는 컴퓨터에서 2진수를 저장하는 방식에 대해 알아보아야 한다.

고정 소수점과 부동 소수점

두 가지 방식은 컴퓨터가 실수를 저장하기 위해 사용하는 사용하는 방식이다. 두 가지 방식의 차이점에 대해 알아보자.

고정 소수점

고정 소수점은 소수 부분의 자릿수가 고정되어 있는 소수 표현 방식이다.
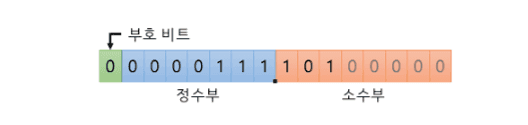
소수점 이하의 자릿수가 고정되어있고 그 자릿수만큼의 비트를 할당하여 표현할 수 있다. 정수부와 소수부를 나누어서 각각을 특정 비트로 할당하는 방식이다.

예를들어 16비트 체계에서 고정 소수점 형식은 앞에서부터 순서대로 부호비트 1비트 정수부 7비트 마지막으로 소수부 8비트로 구성되어 있다.

고정 소수점은 특정한 범위의 값을 표현하거나 계산하는 데 적합하다. 그러나 소수부의 크기가 8비트로 비교적 작은편이라 큰 숫자를 표현하는데 한계가 있다.

만약 소수부에 표현할 수 있는 8비트에 대해 더 적으면 Underflow 에러가 발생하고 8비트를 넘게되면 Overflow 에러가 발생한다.

부동 소수점

부동 소수점은 소수 부분의 자릿수가 고정되어 있지 않고 가변적인 소수 표현 방식이다.

소수를 표현할 수 있는 길이가 가변적이어서 매우 크거나 작은 값들의 다양한 범위의 값을 표현할 수 있다.
초기의 부동 소수점 표현방식은 컴퓨터마다 서로 다른 형식을 사용했지만 현재는 IEEE 표준에 따라 IEEE 754 형식을 따르고 있다.

32비트 기준으로 부호비트 1자리, 지수부 8비트 그리고 가수부 23비트로 구성된다.
첫 부호는 0 양수, 1 음수로 고정 소수점과 동일하다.

지수부는 n의 제곱을 나타내는 수. 즉, 지수위에 달려있는 숫자를 뜻한다. (2^n제곱)

위에서 예제로 살펴본 52.625의 이진수 110100.101 (2)은 부동 소수점 형태로는 어떻게 저장하는지 살펴보자.

110100.101 에 대해 1의 위치를 찾는다. 이 과정을 정규화라고 하는데 1.10100101 × 2^5 와 같이 정규화하게 된다. 여기서 5는 이진수에서 소수점을 이동시킨 비트 수이다.

양수이므로 부호비트는 0으로 설정된다.

지수부는 정규화된 이진수 에서 소수점 이동 비트 수에 특정한 오프셋을 더한 값으로 지정한다. 5의 경우 양수이므로 IEEE 574 표준에 따라 127을 더한다.

5 + 127 = 132 (10) → 10000100 (2)

이렇게 생성된 최종 값은

부호비트 0
지수부 10000100
가수부 10100101 이 된다.

32비트 기준으로 빈 공백에 0을 채우고나면

01000010010100101000000000000000 이 된다.

결론

그래서 왜 0.1 + 0.2 ≠ 0.3 이냐는 최초 질문에 대해 이제 답할때가 왔다.

0.1을 부동소수점 방식으로 바꿔보자.
0.1을 2진수로 바꾸면 딱 나누어 떨어지지 않기 때문에 0.0001100110011001100…. 이 반복된다.
0.2 역시 동일하다. 딱 나누어 떨어지지않고 0.0011001100110011001100… 이 반복된다.

나누어떨어지지 않는 이 2개의 소수는 부동소수점 방식으로 메모리에 저장하면서 제일 뒤 숫자를 잘라내고 근사치로 저장할 수 밖에 없다.

그러면 어떤일이 발생할까?

의 값이 나오게 된다.

실제로 이 값은 0.3 일까?

0.3을 2진수로 바꿔보면 0.010011001100110011001100110011001100110011001100110011 이다.

위에서 구한 0.1 + 0.2 와 0.3 을 비교해보자.

0.1과 0.2를 2진수로 바꾸는 과정에서 딱 나누어 떨어지지않고 무한소수로 변환되어 한정된 메모리 저장소에 저장하기위해 뒤를 짜르고 근사치로 저장하게 된다.

그 결과로 0.3의 2진수와 비교해봤을 때 아주 작은 수의 차이가 생기게 된다.
결국 처음 봤던 0.1 + 0.3 ≠ 0.3 의 결과를 확인할 수 있다.