책에서 목차 찾기

책을 펼쳐보면 대부분의 책에는 목차 가 존재한다.
목차는 왜 있는것일까?

책에는 목차가 존재한다

목차가 있다면 찾고자 하는 내용을 더 빠르게 찾을 수 있다.

어떠한 내용에 대해 찾고 싶을 때 목차를 통해 대략 M~N page안에 있겠구나~ 라고 생각하고 해당 페에지에서 찾아본다면 내용을 빠르게 찾을 수 있을 것이다.

책의 목차가 존재하기도 하지만 내가 정확한 위치를 알고 있다면?

목차가 존재하더라도 만약 찾고자하는 내용이 책의 M페이지에 있다! 라는걸 정확히 알고있으면 어떨까?
바로 해당 페이지로 책을 펼치면 가장 빠르게 원하는 내용을 찾을 수 있을 것이다.

책에 목차가 존재하지 않는다면?

책에 목차가 존재하지 않는다면 어떤일이 발생할까?

내가 찾고자 하는 내용을 책의 어디에 있는지 알 수 없기 때문에 책의 1페이지부터 찾기 시작해야 할 것이다. 내가 찾고자 하는 내용이 책의 마지막에 있는 경우라면 최악의 경우에 책의 모든 페이지를 뒤져야만 내가 원하는 내용을 찾을 수 있을 것이다.

Index

위에서 살펴본 책의 목차가 사실 Index의 존재 이유를 그대로 표현하고 있다. 우리는 데이터베이스에 수많은 데이터를 저장하고 불러오고 수정하고 또 삭제한다.

그 과정에서 수많은 데이터 중에 내가 원하는 데이터를 어떻게, 더 빠르게 찾아낼 것인가에 대한 문제이고 그 과정에 Index라고 하는 것을 사용한다.

오늘 Index가 어떻게 동작하는지 살펴보고, 동작원리를 살펴봄으로써 Index 사용할 때 주의사항에 대해서도 정리해 보고자 한다.

오늘 소개하는 Index 자료는 MySQL에서 사용하는 B-Tree를 기준으로 설명한다. B-Tree를 사용하지 않는 다른 Database의 경우 Index의 동작원리가 다를 수 있음을 명시한다.

Clustered Index VS Non Clustered Index

Index에는 크게 Clustered Index와 Non Clustered Index 두가지로 나눌 수 있다.

먼저 Clustered Index는 개발자가 설정하는 Index가 아닌 MySQL이 자동으로 설정하는 Index이다.

1. 해당 테이블에 Auto increments 값으로 PK가 있다면 해당 컬럼이 Clustered Index가 된다.
2. 만약 해당 PK가 없다면 컬럼 중에 Unique컬럼을 Clustered Index로 선정한다.
3. unique컬럼도 하나도 없다면? MySQL에서 내부적으로 Hidden Clustered Index Key (row ID)를 만들어 Clustered Index로 사용한다.

MySQL에서 Clustered Index Key로 사용하는 위 3가지 조건을 살펴보면 공통점이 있다.
바로 테이블의 count(*) 와 distinct key 한 값이 똑같다는 것.
그 이유는 모든 row를 통틀어 중복이 적으면 적을수록 Index는 높은 효율을 자랑한다. 그 이유는 또 뒤에서 살펴볼것이다.

이떄문에 MySQL에서 자동으로 설정되는 Clustered Index는 최대 효율을 위해 중복이 최대한 발생하지 않는 컬럼을 사용하게 된다.

다음으로 Non Clustered Index가 있다.
Non Clustered Index는 개발자 또는 DBA등이 설정하는 모든 Index는 Non Clustered Index에 해당한다.

멀티 컬럼 Index의 경우 최대 16개의 컬럼을 사용할 수 있고, 테이블당 인덱스의 개수는 최대 64개까지 지정이 가능하다. (Clustered Index까지 한다면 총 65개)

B-Tree Node (Page)

MySQL에서는 Index 의 저장 구조로 B-Tree를 사용한다.
이진트리 < B-Tree < B-Tree 순으로 확장되어진 자료구조라고 이해하면 되고, B-Tree와 B-Tree에 대해서는 별도의 포스팅으로 다뤄보고 이번에는 B-Tree에 대해서만 소개한다.

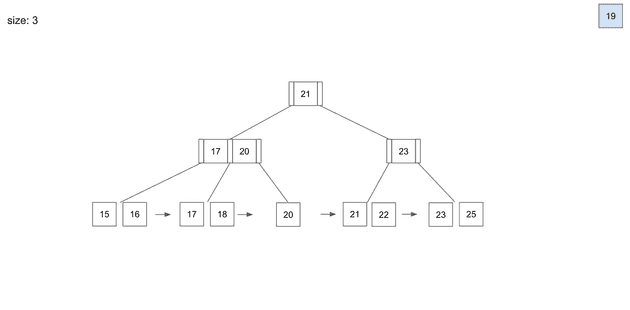
먼저 B-Tree를 소개하기전에 왼쪽에 B-Tree의 구조를 살펴보자.
각각의 사각형 한개 한개를 Node 혹은 Page라고 부르고 MySQL에서는 Page의 사이즈가 16KB로 설정되어있다. (my.cnf에서 수정은 가능하지만 16KB일 때 가장 큰 효율이 난다고 한다. 왜 그런지는 별도의 포스팅에서 작성해보도록 한다.)

Node 중에서 최 상단 레벨에 존재하는 Node를 root node라고 하고 최 하단에 디스크의 주소를 가지고 있는 node 레벨을 leaf 노드라고 한다. 그리고 root와 leaf 사이에 있는 node들을 branch node라고 부른다.

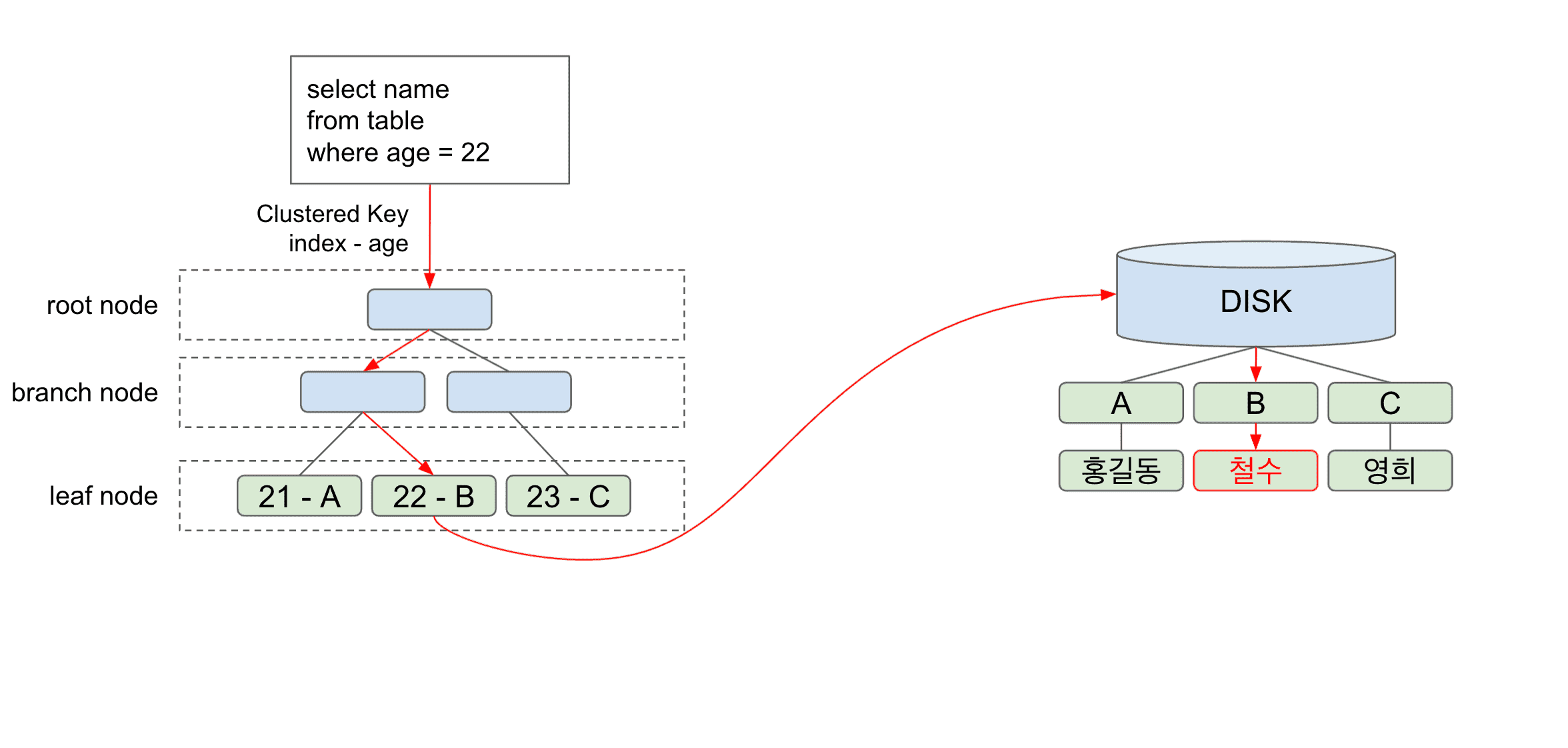
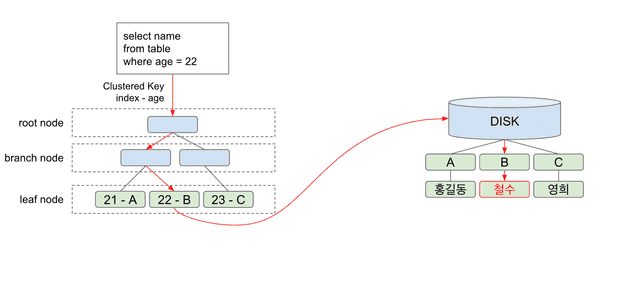
예제로 가져온 쿼리를 살펴보자.

select name from table where age = 22;

간단한 쿼리이다. age 컬럼이 index로 설정되어 있다고 가정하고 이 쿼리에서 index를 통해 데이터를 어떻게 조회해오는지 살펴보자.

우선 root node로 가서 age = 22인 값의 leaf노드로 가기위한 경로를 안내받는다.
root node는 branch node의 경로를 안내해주고 (branch node가 없어서 root node 바로 아래 leaf node가 있다면 바로 leaf node의 위치를 알려줄 것이다.) branch node로 가면 또 아래의 branch node혹은 leaf node의 경로를 알려줄 것이다.

그렇게 leaf node까지 도착하게 되면 leaf node는 index 의 값과 디스크의 주소값을 가지고 있다.

만약 위 쿼리에서 select name 이 아닌 select age로 조회했으면 어떨까?
B-Tree 를 통해 age값이 22인걸 이미 알고있으니 디스크로 접근할 필요가 없다.

하지만 우리는 age가 아닌 name을 조회했기 때문에 디스크까지 접근해야한다.
이 때 디스크 I/O가 발생하고 age 22에 저장되어있는 디스크 B주소로 접근하게 된다.

그러면 최종적으로 디스크 B주소에 있는 철수 라는 데이터를 가져오고 조회결과를 보여주게 된다.

데이터양이 많아질수록 더 빨리지는 Index 검색

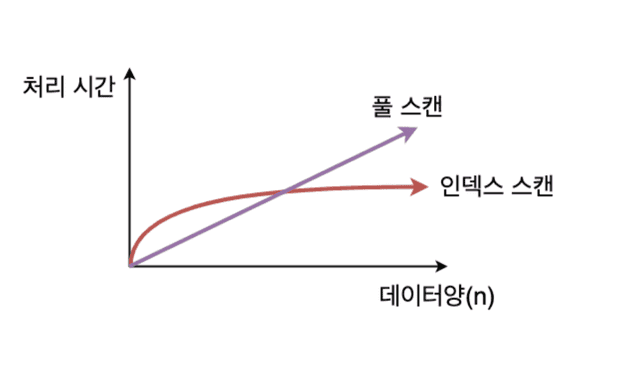
Index로 설정해두면 데이터양이 많아질수록 full scan보다 index scan이 더 빠르다.
간단하게 위 그래프로 살펴보자.

특정 데이터양의 시점까지는 Full scan이 더 빠르다가 그 이후로는 Index scan이 더 빠르다.

Index scan보다 Full scan이 더 빠르다고?

위 그래프에서 보면 특정 시점까지는 Full Scan이 오히려 더 빠르다.
그 이유가 무엇을까?

위에서 살펴보았듯이 Index를 통한 검색은 B-Tree에서 leaf node까지 찾아 내려간 후 해당 데이터를 찾기위해 disk로 접근한다.

그런데 Full scan은 이렇게 B-Tree를 찾아가는 과정이 없다. 디스크로 가서 바로 모든 데이터를 읽어온다.

1. 데이터 양이 많지 않거나, Index가 효율적으로 설정되어있지 않은 경우 오히려 Table Full scan이 더 빠르다.

2. 그리고 Index Full Scan이 실행되는 경우 Index Full Scan의 데이터가 테이블의 모든 데이터의 양과 비슷한 경우에도 역시 Table Full Scan이 더 빠를 수 있다.

B-Tree의 데이터 삽입

B-Tree에서 데이터가 삽입되는 과정을 살펴보자.

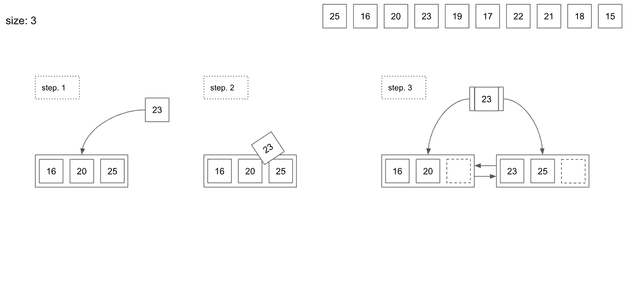
위에서 page size 는 16KB라고 했지만, 예제로 살펴보기 위해 우리는 한개의 node는 최대 3개의 데이터를 저장할 수 있다고 가정한다.

데이터 삽입을 살펴보기 전에, 간단하게 B-Tree에 page에서 데이터가 overflow 발생했을 때 어떤 일이 일어나는지 간단히 살펴보자.

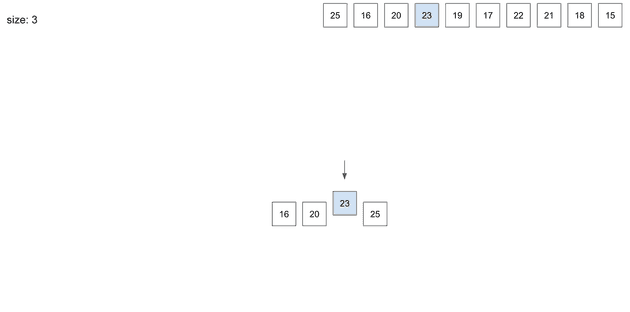
Step1에서 이미 3개가 들어있는 page에 새로운 데이터인 23이 들어오려고 한다.
index는 모든 데이터가 정렬된 상태로 저장하기 때문에 23은 20과 25 사이에 들어가려고 할것이다.

그런데 데이터 개수가 넘치기 때문에 page split과정이 일어나게 된다.
split이 발생하면서 1개의 데이터가 상위 node로 올라가게되고 해당 node는 leaf node를 가지키는 page number를 저장하게 된다.

어떤 데이터가 상위 node로 올라가는걸까?

B-Tree기준으로는 예제에서 데이터사이즈가 3개인 경우 새로운 데이터가 들어오면서 4개가 된 경우 n/2+1 번 째의 데이터가 상위로 올라간다. 즉 4/2+1 = 3 3번째 데이터이므로 Step3처럼 23이 상위로 올라간다.

그렇다면 page에 데이터 저장개수가 짝수개라면? n/2의 위치의 데이터가 상위 node로 올라간다.

page merge

page에 데이터가 넘치는 경우 page가 2개로 나눠지는. 즉, split과정이 일어난다.
또 반대로 3개를 저장할 수 있는 page에 1개씩만 저장된 page가 많다고 가정해보자.
(이런 경우는 데이터를 삭제하는 경우에 발생할 수 있다)

이런경우에는 공간낭비를 줄이기 위해 MySQL이 2개의 page를 1개로 병합하는 merge 동작이 일어난다.

B-Tree의 데이터 삽입 예제

그럼 한 단계식 B-Tree에 총 10개의 데이터를 넣어보자.

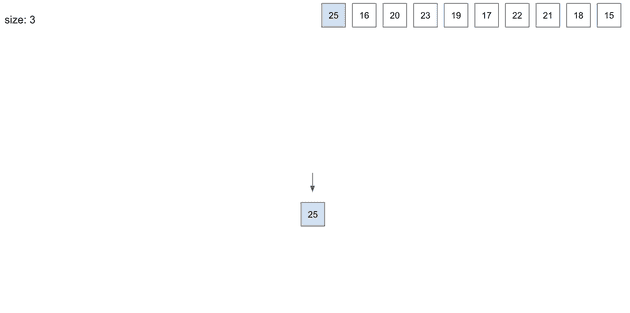
insert(1) - 25

먼저 첫 번 째 데이터인 25를 넣어보자.

node에는 총 3개의 데이터를 저장할 수 있고 자리가 매우 널널하다. 25가 그대로 저장되고 종료된다.

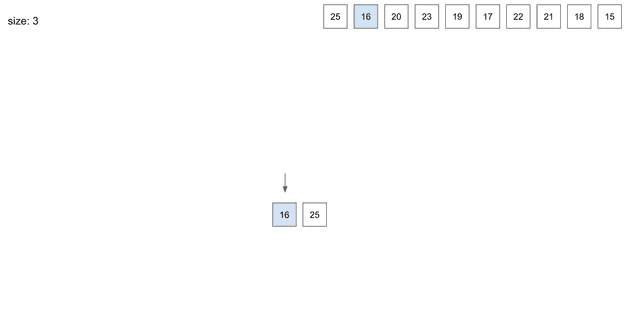
insert(2) - 16

다음으로 16을 넣어보자.

Index는 항상 정렬된 순서로 저장한다. 그렇게 때문에 이미 저장된 25보다 왼쪽에 저장된다.

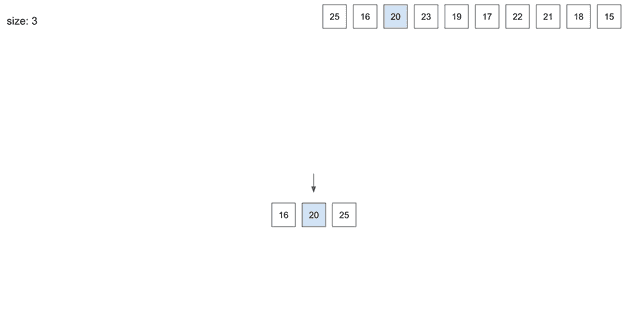
insert(3) - 20

다음으로 20을 넣어보자.

16과 25 사이에 저장된다.

insert(4) - 23

다음으로 23을 넣어보자.

23을 넣으려고 봤더니 page size가 꽉 차는 상황이 발생했다.
n/2+1에 의해 3번 째 데이터는 23이 상위 node로 올라가야 한다.

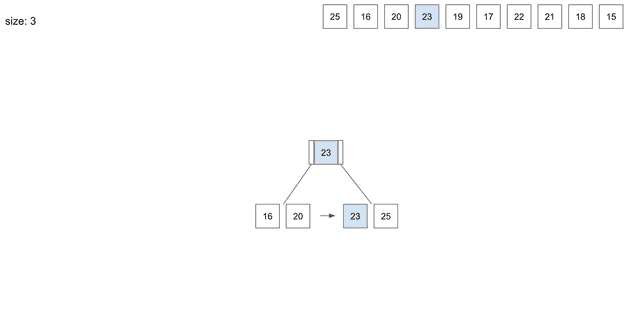23이 상위 node로 올라가면서 root node와 leaf node 2단계로 나뉘어졌다.

insert(5) - 19

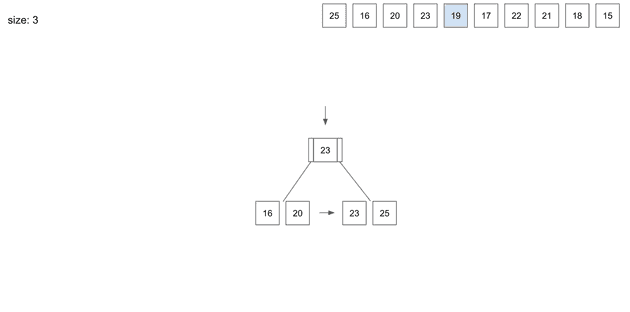이제는 root node가 있으니 데이터가 바로 저장되지 않는다.
root node부터 19를 저장하기 위한 leaf node를 찾아야한다.

먼저 root node에 있는 23에게 가서 19가 가야할 leaf node의 위치를 확인한다.
19는 23보다 작기 때문에 왼쪽의 leaf node의 위치를 알려줄것이다.

그러면 root node의 왼쪽 경로를 따라 내려가서 만난 leaf node에 19를 저장하게 된다.

insert(6) - 17

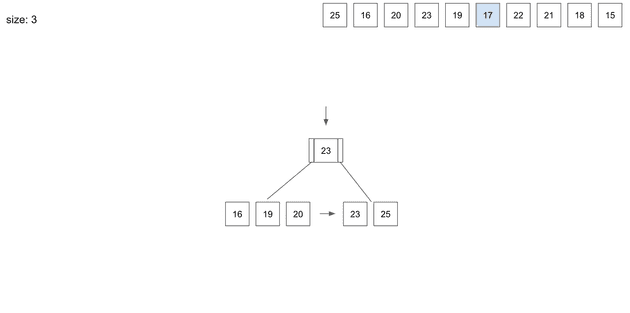17을 넣기위에 동일하게 root node부터 탐색한다.
역시 왼쪽 leaf node로 따라 간다.

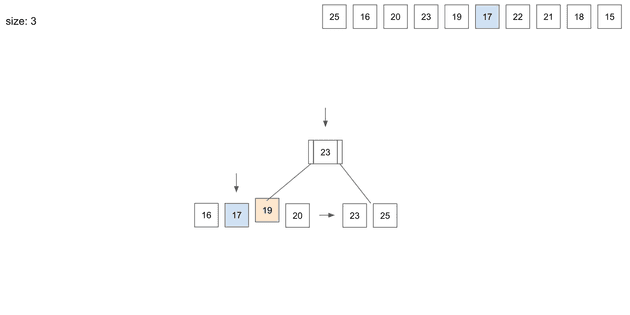17을 저장하고 보니 page가 넘치는 문제가 발생해서 split과정이 일어난다.

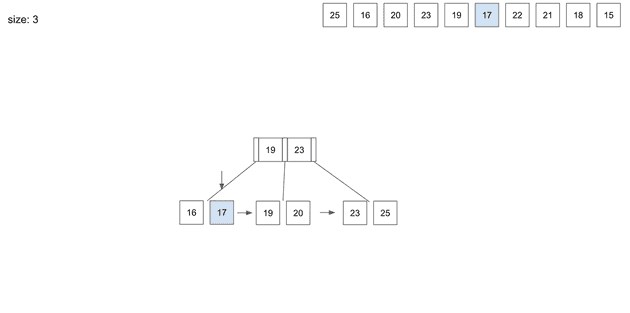3번째 자리에 있는 19가 상위 node로 올라가게 된다.

insert(7) - 22

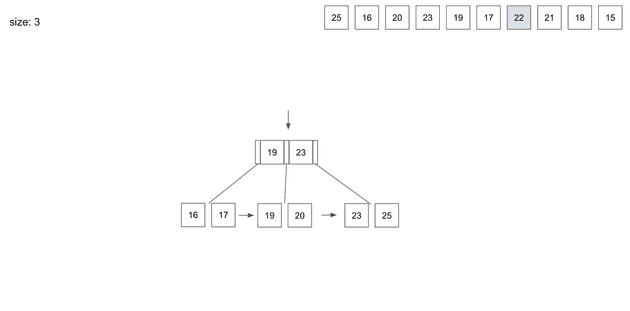22를 저장하기위해 root node를 살펴보면 22는 19와 23의 사이값이다.

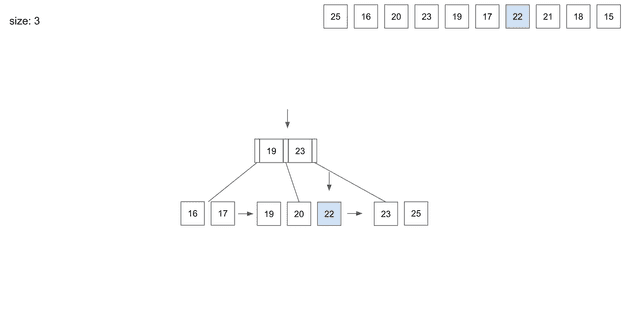root node에서 알려준 가운데 leaf node로 와서 22데이터를 저장한다.

insert(8) - 21

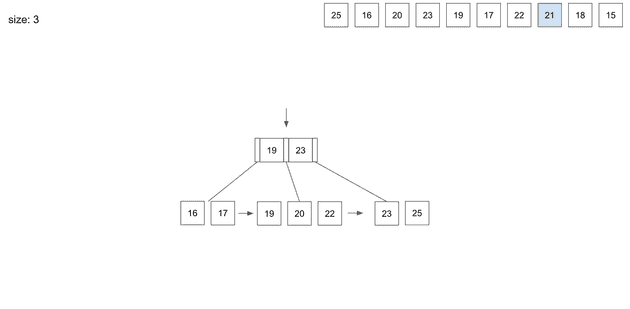21을 저장하기위해 root node에서 경로를 찾아간다. 가운데 leaft node를 알려줄 것이다.

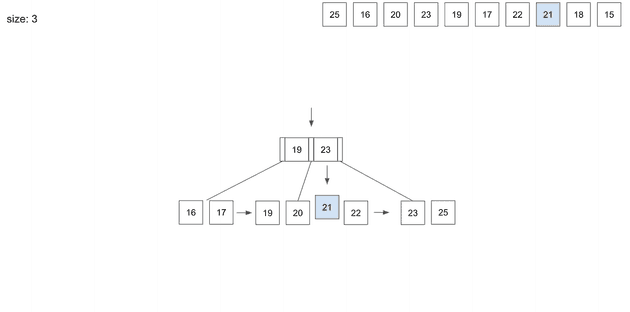21을 저장하고보니 페이지 사이즈가 넘치게 되어 split이 일어났다.

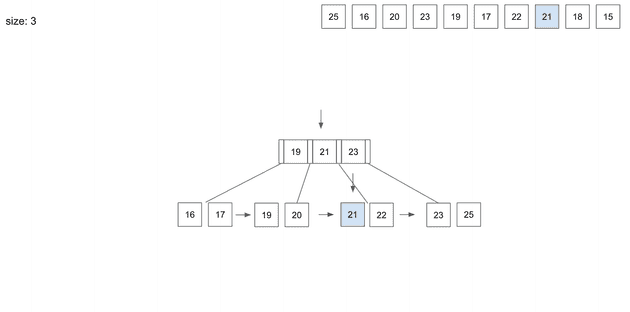3번째 데이터인 21이 상위 node로 올라가게 된다.

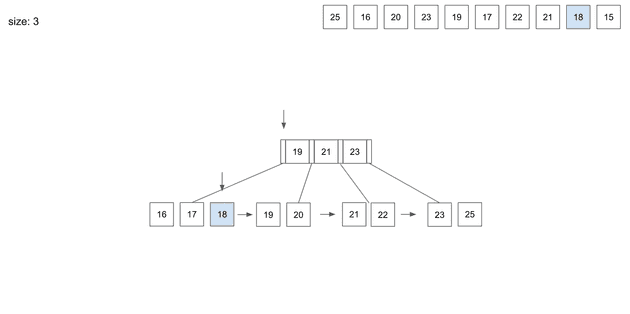
insert(9) - 18

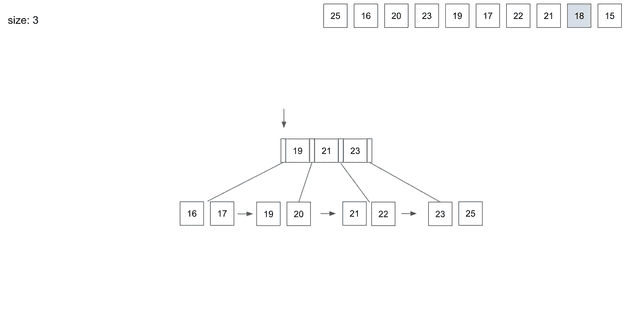18을 넣기위해 root node를 살펴보면 가장 왼쪽 경로를 통해 leaf node를 찾아간다.

자리 공간이 있으니 18을 저장하고 종료한다.

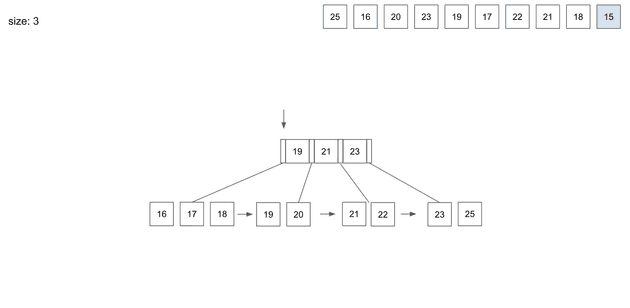
insert(10) - 15

마지막으로 10번째 데이터인 15을 넣어보자.

역시 19보다 작으니 가장 왼쪽 경로를 따라 찾아가게 된다. 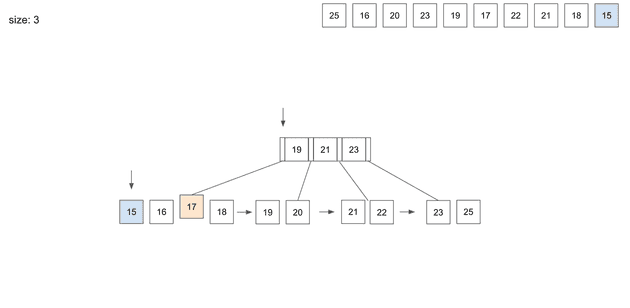15를 저장하고보니 leaf node의 split이 필요하다.

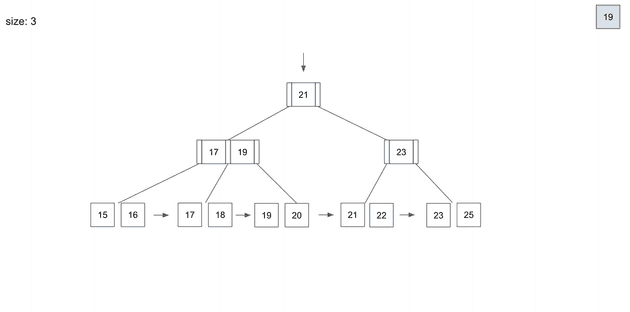
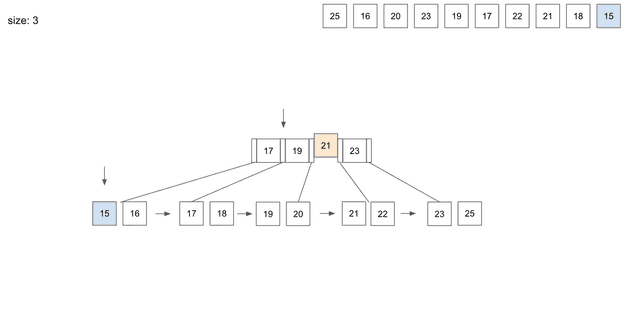split을 통해 leaf node를 두개로 나눴고 17을 상위 node로 복사했다.
그런데 이번에는 또다른 문제가 발생했다.

상위의 root node에서 page가 넘치는 상황이 생겼다.

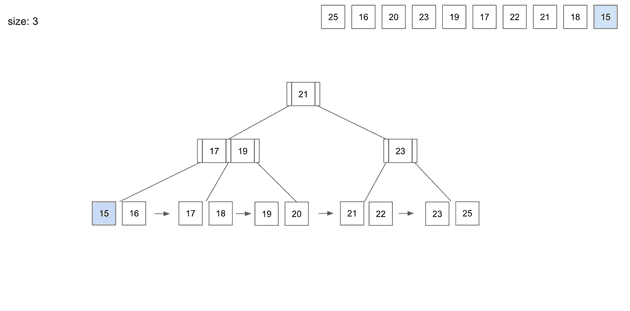상위 root도 동일한 조건으로 split 과정이 일어난다.

여기서 leaf node와의 split차이점은 상위로 데이터를 저장할 때 중복으로 저장하지 않는다.
그 이유는 leaf node는 모든 데이터와 디스크 주소값을 가지고있는 반면,
B-Tree에서 root node와 branch node는 하위 node의 경로값만 가지고 있다.

이제 root, branch, leaf 3단계가 모두 있는 B-Tree 구조가 되었다.

delete - 19

이번에는 데이터를 삭제해보자.

데이터를 삭제할때도 insert할때와 동일하게 root node부터 leaf node를 찾아가는 과정은 동일하다.

19라는 데이터를 삭제해보자.

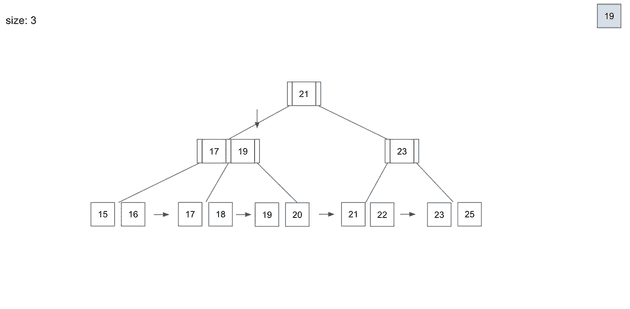역시 root node -> branch node -> leaf node 순서로 데이터의 위치를 찾아갈 것이다.

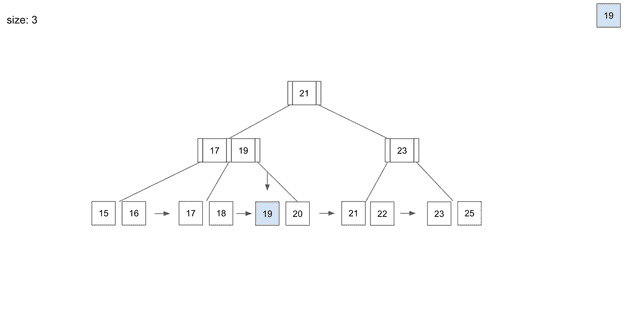19라는 데이터를 찾았을 때 index에서 해당 데이터를 삭제한다.

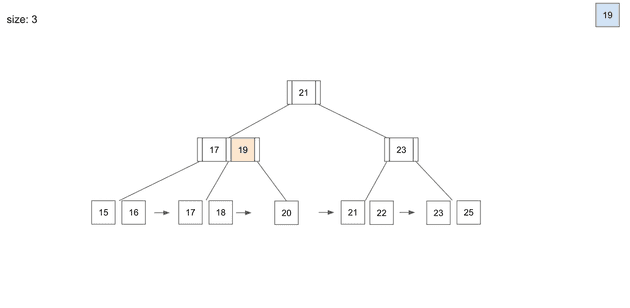19를 삭제하고보니 여기서 문제가 발생한다.
branch node에서 19를 가리키고 있었는데, 19라는 데이터가 삭제되었다.

이 경우 branch node는 해당 leaf node에서 가장 작은 값인 20으로 다시 저장하는 동작이 일어난다.

branch node의 값을 20으로 바꿔주고 삭제 작업이 끝나게 된다.

update

B-Tree에서 insert와 delete의 과정을 위에서 살펴보았다.
B-Tree에서 update라는 명령은 없다. 그렇다면 update는 어떻게 동작하게 될까?

바로 update를 실행하게 되면 delete -> insert 순으로 동작이 일어난다.

이 과정에서 delete를 하면서 page에 빈 공간이 많아질 경우 두 page가 합쳐지는 merge과정이 발생할 수 있고,
위에서 살펴본 것 처럼 leaf node를 가지키고있는 값이 삭제되는 경우 branch node가 가리키는 값을 바꿔야하는 경우가 발생할 수 있다.

Index 컬럼의 설정

제일 앞에서 Index는 조회속도를 빠르게 하기위해 사용한다고 했는데, 그렇다면 조회 속도를 높이기 위해 Index는 많으면 많을수록 좋은걸까?

B-Tree의 동작과정을 살펴보았다.
B-Tree의 동작과정을 다시 한 번 생각해보면 위 질문에서 답변이 아니요 라는것을 알 수 있다.

select는 index에 의해 더 빨라지겠지만, update, delete, insert의 동작이 더 느려지게 될것이다.
새로운 데이터가 생겼을 때 index1개면 위 과정이 1번이겠지만 index가 20개라면 20번 실행되어야 한다.

그렇다면 어떤 컬럼에 Index를 설정하면 좋을까

이 질문 역시 앞에서 설명한 내용으로 답변할 수 있다.

MySQL에서 자동 설정하는 Clustered Index의 조건을 다시한번 생각해보자. 테이블에서 모든 row에 중복이 적으면 적을수록 좋다.

카데널리티가 높은 컬럼이 좋다. 즉 데이터의 중복이 적으면 적을수록 좋다. discint foo 했을 때 랑 count(*) 가 비슷한 컬럼일수록 Index 효율이 높다.

index의 손익분기점이라고 표현하는데, 상황에 따라 다르겠지만 보통 전체 데이터의 5 ~ 10% 정도로 걸러지는 경우 index를 사용했을 때 좋은 효율을 낼 수 있다.
이 내용은 테이블의 데이터가 100만건 정도일 때 조건이고, 1000만건 그 이상 많아진다면 손익분기점은 더 낮아진다. 1000만건 이상인 테이블에서는 보통 5%정도로 걸러져야 효율이 좋다.

그리고 20%가 넘어가는 경우 오히려 Table Full Scan이 더 빠를 수 있다.

그리고 당연하게도 활용도가 높은 즉, 많이 사용되는 컬럼을 Index로 사용하는게 좋을것이다.

Index로 설정했지만 왜 Full Scan으로 동작할까?

MySQL의 경우 explan을 통해 쿼리가 어떻게 실행되는지 살펴볼 수 있다.
분명 where 에 index컬럼을 사용했지만 full scan으로 동작한다.

왜 그럴까? 많이 실수하는 몇가지 이유를 살펴보자.

컬럼의 가공

B-Tree는 해당 Index의 데이터값을 그대로 저장하고 있다. 그런데 데이터를 가공하여 바교하는 경우 Index를 통한 검색이 불가능하다.

ex) where price * 0.9 > 10000

==>

where price > 10000 / 0.9

price가 index로 설정되어있다고 하더라고 price * 0.9에 대한 결과값은 알 수 없다. 따라서 위 쿼리의 경우 아래처럼 0.9를 오른쪽으로 보내어 쿼리를 실행해야 index를 통한 검색을 할 수 있다.

!= (부정형)

부정형으로 where을 사용하는 경우 해당 데이터를 제외한 모든 데이터를 검색해야 한다. full scan으로 동작하는 사례이다.

like 앞 %

B-Tree는 데이터의 첫 글자를 기준으로 정렬하여 저장하고 있다. 그런데 like쿼리를 통해 앞에 %를 붙이는 경우 모든 데이터를 찾아야하는 Full Scan으로 동작하게 된다.

count(*)

count(*) 라는건 모든 데이터를 한바퀴 돌아야 몇개인지 알 수 있다. 따라서 Full scan으로 동작한다.

멀티 컬럼에서 두번째 컬럼을 조건으로 사용하는 경우

예를들어 age, name 으로 멀티 컬럼 index가 설정된 경우 B-Tree는 age로 정렬한 후 name으로 정렬한 데이터를 저장하고 있다.

그런데 name만을 조건으로 사용하면 Index를 통한 검색을 할 수 없다.
(반대로 age가 첫번째 조건이기 때문에 where age만 하면 Index검색이 된다.)

멀티 컬럼 Index에서 순서를 바꾸는 경우

age, name 순으로 인덱스를 지정하고나서 where name, age로 조건을 주는 경우,
B-Tree는 age, name순으로 정렬된 데이터를 가지고있기 때문에 Index검색을 할 수 없다.

(반대의 순서로 where을 주더라도 Database에 존재하는 옵티마이저가 컬럼 순서를 바꿔서 조회한다. 따라서 index검색이 되기는 한다. 옵티마이저가 없다면 Index로 실행되지 않는 경우이다.)