JavaScript로 풀어보는 graph 탐색 알고리즘 (BFS)

author

postNo

status

thumbnail

description

Graph 탐색 알고리즘

우선 graph의 탐색 알고리즘에는 크게 두 가지가 있다.

깊이 우선 탐색 (Depth First Search)

너비 우선 탐색 (Breadth First Search)

오늘은 두 번째인 너비 우선 탐색 알고리즘중에 가장 유명한 문제인 최단거리 찾기에 대해 설명해보고자 한다.

설명

주어지는 m x n 크기의 배열에서 시작점 0, 0에서부터 m-1, n-1 위치까지 가는 가장 짧은 거리의 비용을 출력하라.

배열에 표시된 값은 해당 칸으로 이동하기 위한 비용을 의미한다.

예제

1	0	1	1	1
:---:	:---:	:---:	:---:	:---:
1	0	1	0	1
1	10	1	8	1
1	0	1	0	1
1	1	1	0	1

</div>

답

설명

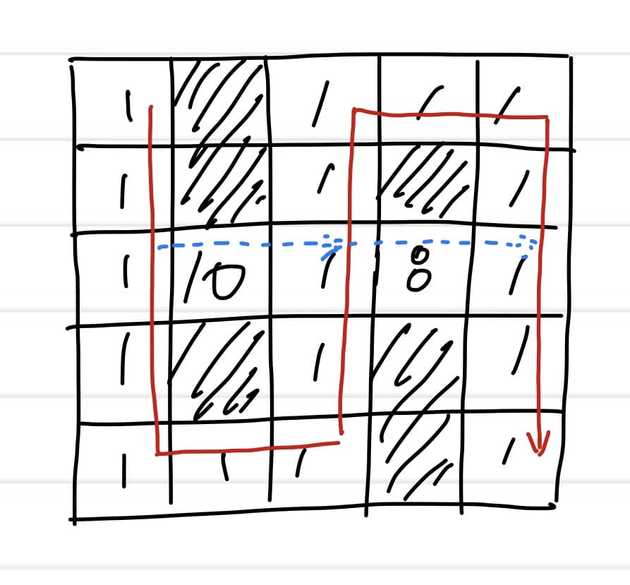0, 0에서 이동가능한 위치는 여러개가 있지만 가장 최소 비용으로 이동할 수 있는 길은 빨간색으로 표시한 한 가지이다.

점선 파란색으로 표시된 길도 있긴 하지만 비용이 높아 빨간색으로 가는 것 보다 더 비싼 비용이 발생한다.

따라서 출발점(0,0)부터 도착점(m-1, n-1)까지 가는 최단 경로는 빨간색이며 비용은 17이다.

JavaScript 코드로 살펴보기

const solution = (maps) => {
  const valueMap = maps.map(i => i.map(v => 0));

  const sizeX = maps.length;
  const sizeY = maps[0].length;

  // L -> R -> D -> U 순서로 순회한다
  const directionX = [-1, 1, 0, 0];
  const directionY = [0, 0, -1, 1];

  const queue = [];

  const startPositionX = 0;
  const startPositionY = 0;

  // set start position
  queue.push([startPositionX, startPositionY]);
  valueMap[startPositionX][startPositionY] = maps[startPositionX][startPositionY];

  while(queue.length > 0) {
    const [x, y] = queue.shift();

    // 4 방향 비교
    for (let i = 0; i < 4; i++) {
      const nextX = x + directionX[i];
      const nextY = y + directionY[i];

      // 표를 벗어난다면
      if (nextX < 0 || nextY < 0 || nextX >= sizeX || nextY >= sizeY) {
        continue;
      }

      // 갈 수 없는 길이라면
      if (maps[nextX][nextY] <= 0) {
        continue;
      }

      // 이미 방문한 곳이고 지금 길이 더 길거나 같다면
      if (valueMap[nextX][nextY] > 0 &&
        valueMap[x][y] + maps[nextX][nextY] >= valueMap[nextX][nextY]) {
        continue;
      }

      valueMap[nextX][nextY] = maps[nextX][nextY] + valueMap[x][y];
      queue.push([nextX, nextY]);
    }
  }

  return valueMap[sizeX-1][sizeY-1] === 0 ? -1 : valueMap[sizeX-1][sizeY-1];
}

결론

똑같지는 않지만 프로그래머스에 비슷한 문제가 있음

https://programmers.co.kr/learn/courses/30/lessons/1844

코드에 대한 오류나 문의는 코멘트나 메일로 남겨주세요!